A grating with high groove density has a high dispersion. This means that the angular separation of wavelengths from the grating is large. It can be desirable to choose a grating with high groove density for two main reasons:
- To obtain a compact design (for a wide wavelength range)
- To obtain a high resolution (for a narrow wavelength range)
However, there is a physical limit to how high the grating groove density can be. In this post we will derive a simple formula for calculating the maximum groove density GMAX for a grating that should cover a certain wavelength range λMIN to λMAX.
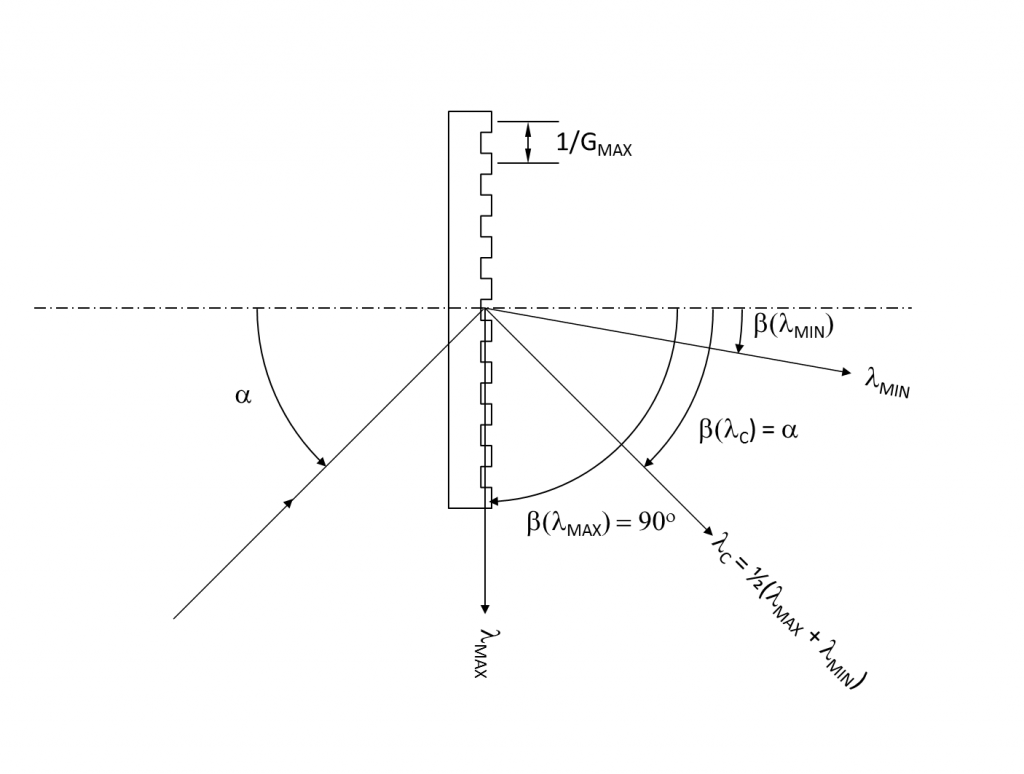
The figure above defines the various parameters and also shows that when the groove density reaches GMAX, the largest wavelength is diffracted at 90 degrees which means the order disappears.
The starting point is the grating as written in the
| Gλ = sin(α) + sin(β) | Eq. 1 |
First of all, we simplify things by assuming the grating is used in Littrow condition at the center wavelength λC = 0.5*(λMAX + λMIN). This means that the diffraction angle β (λC) equals the angle of incidence a at this specific wavelength which means:
| GλC = 2sin(α) | Eq. 2 |
The other condition is that the diffraction angle β equals 90 degrees at λMAX:
| GλMAX = sin(α) + 1 | Eq. 3 |
By combining Eq. 2 and Eq. 3 we finally get the following simple and useful formula for the maximum groove density:
| GMAX = 1 = 4 λMAX – ½λC 3λMAX – λMIN | Eq. 4 |
In reality the groove density needs to be chosen lower that GMAX – typically at 70 – 80% of GMAX
[callout font_size=”12,5px” width=”500″ style=”royalblue”] As an example let us look at a grating for the 800 -1100 nm wavelength range. From Eq. 4 we can quickly calculate that the maximum groove density is 1600 lines per mm. This means, that a practical grating for this range should not have more than approximately 1500 lines per mm.[/callout]